Как страстный энтузиаст математики и человек, который провел бесчисленные часы, погружаясь в мир чисел, я не могу не испытывать восторга от перспективы исследования загадочной и интригующей природы числа Пи. Пи — это больше, чем просто математическая константа; это символ красоты и глубины математики.
🚀 Хочешь улететь на Луну вместе с нами? Подписывайся на CryptoMoon! 💸 Новости крипты, аналитика и прогнозы, которые дадут твоему кошельку ракетный ускоритель! 📈 Нажмите здесь: 👇
CryptoMoon Telegram
Не мог бы День Пи, математический праздник, известный своими празднованиями, связанными с пирогами, отмечаться с большей радостью в летние месяцы?
14 марта, или 14 марта по календарю, мы празднуем День Пи, отмечая первые три цифры известного иррационального числа Пи. Это число, которое часто является первой встречей учеников с иррациональными существами в начальной школе, в настоящее время отмечается в этот особый день. Однако один математик утверждает, что 22 июля было бы более подходящей датой для этого случая.
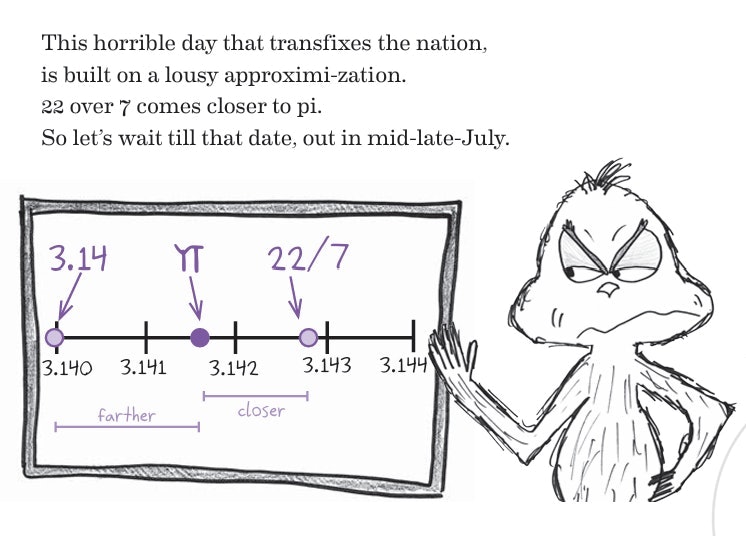
При представлении дат в виде дробей, например 22/7 для 22 июля, это значение на самом деле является близким приближением к числу Пи. На числовой прямой число Пи (3,14) расположено немного ближе к 22/7, чем к его традиционному представлению 3,14. Поэтому, если кто-то хочет быть точным в своих математических наблюдениях, День Пи можно отмечать 22 июля, а не 14 марта.
В своей последней публикации Бена Орлина «Математика для специальностей по английскому языку» (выходит 3 сентября) он углубляется в исследование числа Пи и других математических концепций, предназначенных для тех, у кого еще не развилось сильное пристрастие к числам. . Поскольку математика становится все более распространенной в нашей повседневной жизни, благодаря финансовой грамотности или искусственному интеллекту, приобретение понимания или понимания ее может сделать этот неизбежный, но очаровательный аспект существования более терпимым и приятным.
Это интервью было отредактировано и сокращено для ясности.
Обратное: Прежде всего, что такое число Пи и почему оно так важно в математике?
Пи представляет собой захватывающую пропорцию окружности круга к его диаметру. Проще говоря, чтобы полностью охватить круг, требуется около трех диаметров; точное значение этой математической константы обозначается цифрой «пи».
Когда речь идет о кругах, число Пи является важной константой, которой нельзя избежать. Если вам интересны свойства круга, возможно, вас интересует его диаметр или окружность, или, может быть, вы хотите узнать площадь, которую он покрывает. Для расчета любого из этих значений число Пи играет решающую роль. В математике частыми объектами изучения являются циклические и повторяющиеся закономерности, охватывающие круги, замаскированные под волны, периодичность или повторение. Все эти явления связаны с числом Пи из-за наличия скрытых круговых структур.
Волны – обычное явление в нашем мире. Они отвечают за различные формы общения, такие как звук и свет. Представьте себе, что стрелка часов вращается по кругу. Вместо того, чтобы сосредотачиваться на его положении слева или справа на круге, учитывайте только его вертикальную высоту. Когда вы наблюдаете за стрелкой часов, она движется вверх до самой высокой точки, затем вниз, ниже своего исходного положения, и снова вверх. Эта закономерность повторяется постоянно. Местоположение, на котором вы фокусируетесь, постоянно поднимается и опускается, в результате чего образуется синусоидальная волна — фундаментальная форма всех естественных волн, включая звуковые волны и свет, распространяющийся в пространстве.

Действительно ли 3,14 — лучший способ выразить число «пи»? Если нет, то что?
Я столкнулся с этими математическими концепциями для представления значений целых чисел, таких как дроби и десятичные дроби. Однако ни один из них не может полностью передать суть числа Пи. Пи не равно 22/7, но и не совсем 3,14. Оба приближения не оправдывают ожиданий. Тем не менее, 22/7 немного ближе к цели.
Как математик, глубоко понимающий историю математических концепций, я нахожу удивительным то, как наше понимание и представление таких констант, как число Пи, менялось с течением времени. По своему опыту я заметил, что многим людям трудно понять абстрактную концепцию числа Пи как бесконечной десятичной дроби. Вместо этого я предпочитаю описывать его как «примерно на полпути» между 3,14 и представлением обыкновенной дроби 22/7 на числовой прямой. Эта точка зрения, коренящаяся в старой математической традиции использования дробей, делает эту концепцию более понятной и ее легче визуализировать для меня. Конечно, десятичное представление имеет свои преимущества и необходимо для точных расчетов, но как человек, который ценит как исторический контекст, так и практическое понимание, я нахожу это перефразированное объяснение особенно интересным.
Что вы думаете о Дне Пи?
У меня есть слабость к Дню Пи. Этот необычный праздник, учрежденный в 1988 году Ларри Шоу, физиком из Музея науки в Сан-Франциско, является праздником математики, в частности математической константы Пи. Благодаря своим игривым каламбурам и связям он завоевал всемирную популярность. Однако под поверхностью скрывается глубоко укоренившаяся красота математики. Для достижения такого уровня понимания могут потребоваться некоторые усилия, но как только вы это сделаете, вы оцените сложные взаимосвязи между понятиями, чего иначе трудно достичь.
Это ваша четвертая книга по математике. Что в этом особенного? Что вы надеетесь, что читатели получат от этого?
За время своей работы педагогом и писателем я встречал бесчисленное количество людей – вероятно, более 100, но кто считает? – которые называют себя не энтузиастами математики. По той или иной причине математика не может зажечь их интерес. Эта статья задумана как компактное собрание мыслей, которыми я хотел бы поделиться с этой группой.
В своих предыдущих попытках я сознательно держал математические понятия как можно дальше от школьных занятий. Я выбрал темы, которые казались доступными с простыми английскими объяснениями. Однако я считаю, что эта точка зрения не затрагивает основную проблему: почему многие люди находят математику сложной. Вместо этого я стремлюсь донести, что математика — это отдельный язык, и его освоение включает в себя сложный танец между пониманием идей и пониманием лежащей в их основе терминологии. Книга часто переключается между этими аспектами, и моя цель — провести вас через этот танец, помогая выучить его ритм и шаги.
Что делает число Пи решающим для получения удовольствия от математики для людей, не занимающихся математикой?
Для новичка первая встреча с иррациональным числом может оказаться весьма интригующей. По мере того, как вы привыкаете к математике, новизна иррациональных чисел может исчезнуть. Тем не менее, я ценю вашу точку зрения, как будто вы новичок. С этой точки зрения иррациональные числа поистине необычны. Они обладают уникальной характеристикой, которая отличает их от других чисел.
Что мы еще не понимаем о Пи?
В сфере измерений мы имеем впечатляющий уровень точности, достигающий триллионов цифр. Однако понимание взаимосвязи между этими огромными числами и другими числами сопряжено с некоторыми интригующими нерешенными вопросами. Например, когда вы умножаете числа «пи» и «е», два, казалось бы, знакомых числа, возникают удивительные сложности. Хотя широко распространено мнение, что число Пи, возведенное в степень е, или е, возведенное в степень числа Пи, приведет к иррациональному числу, это не было окончательно доказано. Эти неуловимые цифры продолжают задавать нам простые, но остающиеся без ответа вопросы об их отношениях.
Смотрите также
- «Капитан Америка: О дивный новый мир» наконец-то отвечает на самый большой вопрос Вечных«
- Моя вина: Лондон готовится взорвать Prime Video после огромного успеха Culpa Ma
- Кто такой муж Колмана Доминго Рауль Доминго? Все о его жизни
- Как пройти самый сумасшедший квест Avowed, «Курьер Пустоши»
- Объяснение концовки 6-го сезона «Кобра Кай»: кто победит, кто умрет и что это значит для будущего «Парня-каратиста»
- Американское убийство: Габби Петито: Кто такой Брайан Лаундри? Узнайте, как он связан с истинным преступлением Netflix
- Рабочий человек ТРЕЙЛЕР
- Таннер Бьюкенен и Мэри Маузер помолвлены: узнайте историю любви и хронологию отношений актеров сериала «Кобра Кай»
- Долли Партон объясняет, почему муж Карл Томас Дин избегает посещения с ней мероприятий: «Он любит музыку, но…»
- «Капитан Америка: О дивный новый мир» подготавливает прибытие Росомахи в киновселенную Marvel с помощью адамантовой бомбы
2024-07-22 16:59
